2025江苏高中数学联赛第10题解析

各位同学大家好，我是高中数学刘老师。今天要介绍的这道题目，出自二零二五年江苏高中数学联赛。具体是第十题。我们来看这道题目。

起初提供了两个函数，同时给出了它们的图像，形成了围成封闭曲线c的图形。这两个函数之间存在怎样的联系？实际上它们是彼此的反函数关系。

首先，依照法国的方法，y等于指数函数减去一再加上一，将这个表达式调整，y乘以x等于y加上一减去一。

其次，先解算式x等于y加一减一，再依照对称的规则互换y、x的位置，y就变为loin，括号内是x加一减一，因此正好就是这一段内容。

这两条属于会员逆向关系式，依照会员逆向关系式的特点，其图形必然以一三象限分角线为对称轴。既然具备对称性，一三象限分界线与之对称的便是y等于x直线，这条直线的倾斜度值为负一，显然两者形成直角。相交的两条线段若记作a和b，则它们会取得最大交点。

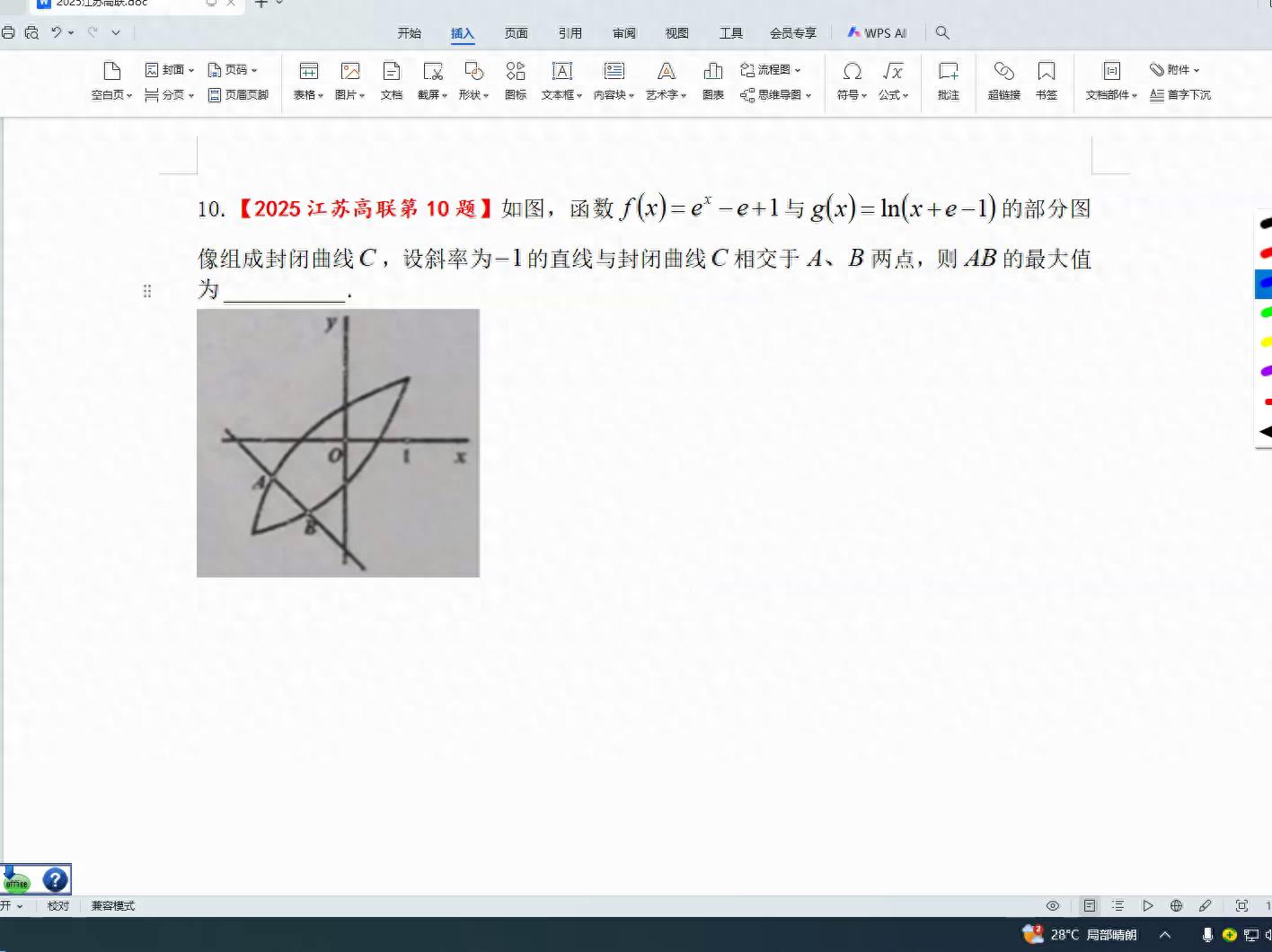
a、b在什么地方才能达到最大？很显然有两种思路。

一种情况是接触，就是和y、d、x构成的那条直线平行的一条线与之接触，接触时，该位置到它的间隔是最大的，因为其他位置都在它的下面，接触点时间隔最大。

另一种相切方式是先去掉x加m，然后确定它与那条线的交点，或者直接找到切点即可，切点非常容易确定，因为f对x的导数等于e的x次方，切点的坐标是x零y零，此时e乘以x零不等于一，x零等于零，xc零表明切点后的坐标为零，正坐标应该是二减一，二减一其实这个点图像画得不够精确。

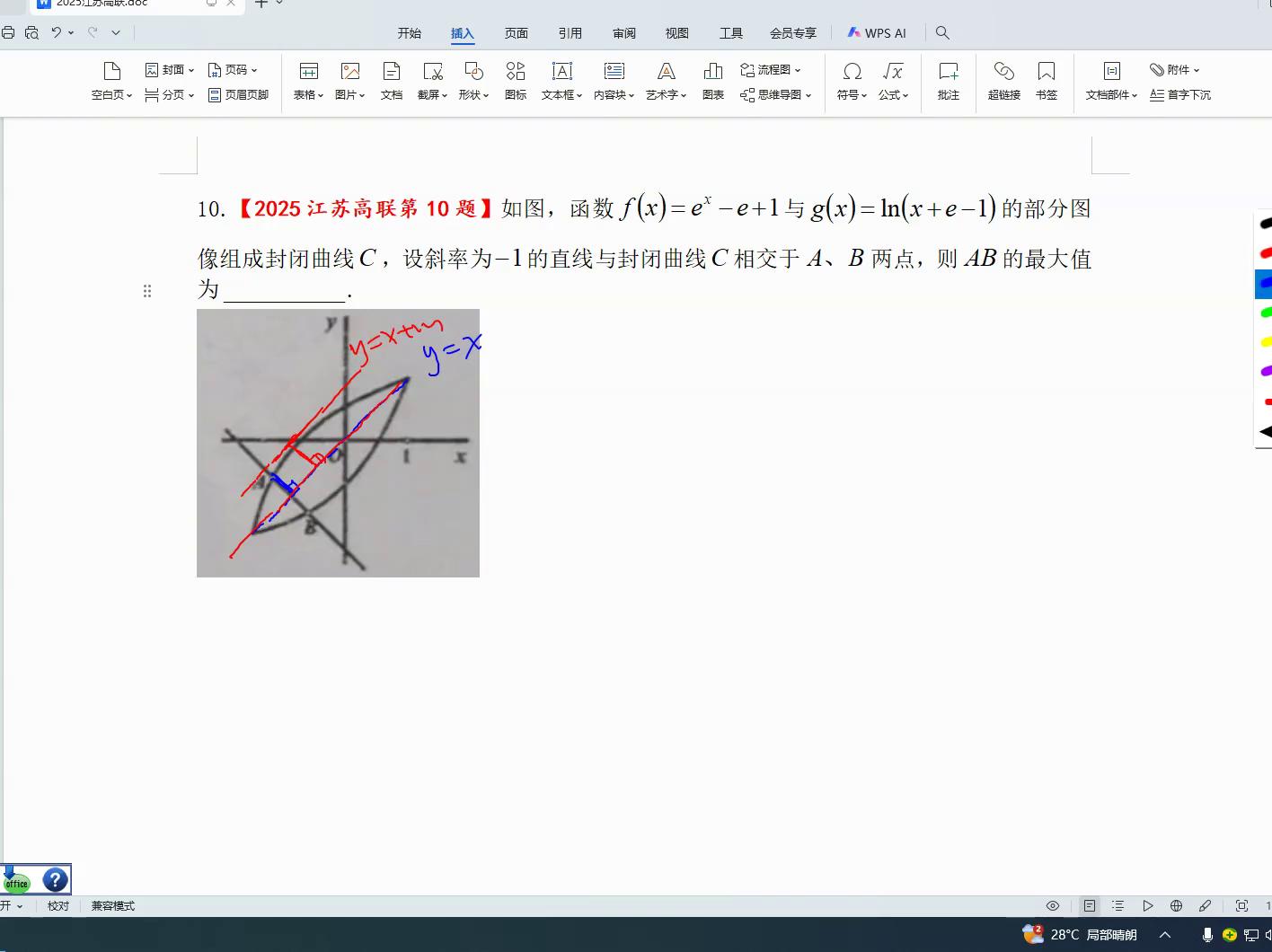
这个点已经确定，根据两点间距离公式，y的值是否等于y减去x后等于零点到某点间距离的公式，即二减一绝对值除以根号二，这就是这个距离的最大值是多少，最大距离最终再乘以二。

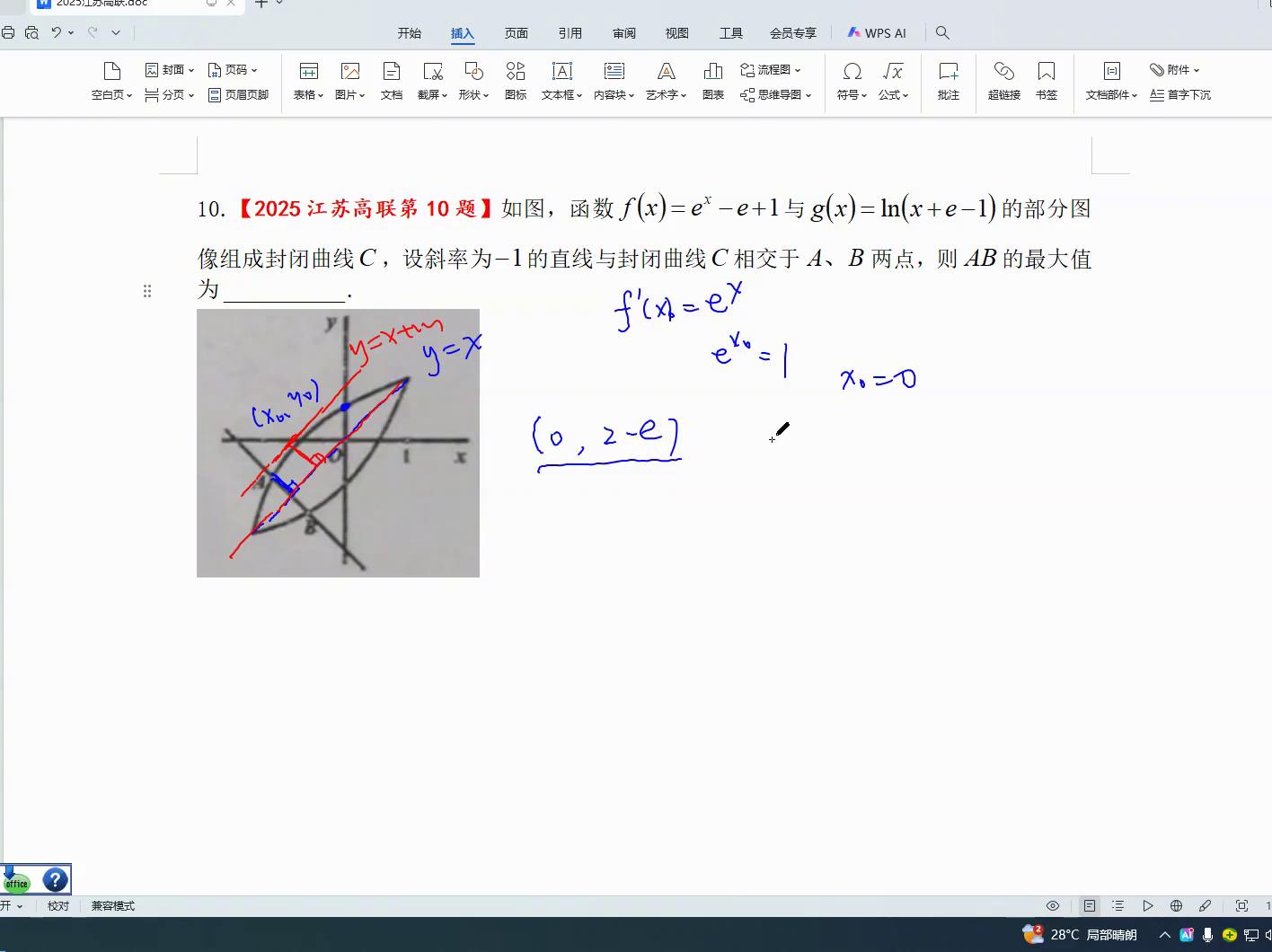
那是什么原因呢，首先它是镜像的，其次它要算出i点到b点的最大距离，这个距离再乘以二，再乘以二，最后得出的答案就是根号下两倍的跨上减去二，因为二比一要小，所以就是这样的结果。

这种方式，除了借助先前的思路去领会以外，还可以直接进行设定，因为存在一条对称轴，直接设a点到该轴的距离，a点坐标为x零二零点五二零，即e x零减一加一，直接应用这个点到y减x零零直线的距离，就是前面绝对值一x零减x零减一加一，除以二，最后当然再乘以二。

为何要倍增数值，是由于确定了一个a位置，b位置与之呈镜像关系，b位置与a位置互为镜像，接下来要计算，就是求取这个数值的极值，包括最大值与最小值。

观察一个区间，借助hx相当于e的x次方减去x减一再加上一，hdx很轻易算出e的x减一，这时候很容易明白hd在零处等于零，当x等于零，x等于零时也等于零，零在此处必定是个极小值点，极小值点就是此处必定大于等于h零，h零很轻易可以算出，h零计算出来是二减一，h零很轻易地可以算出来。

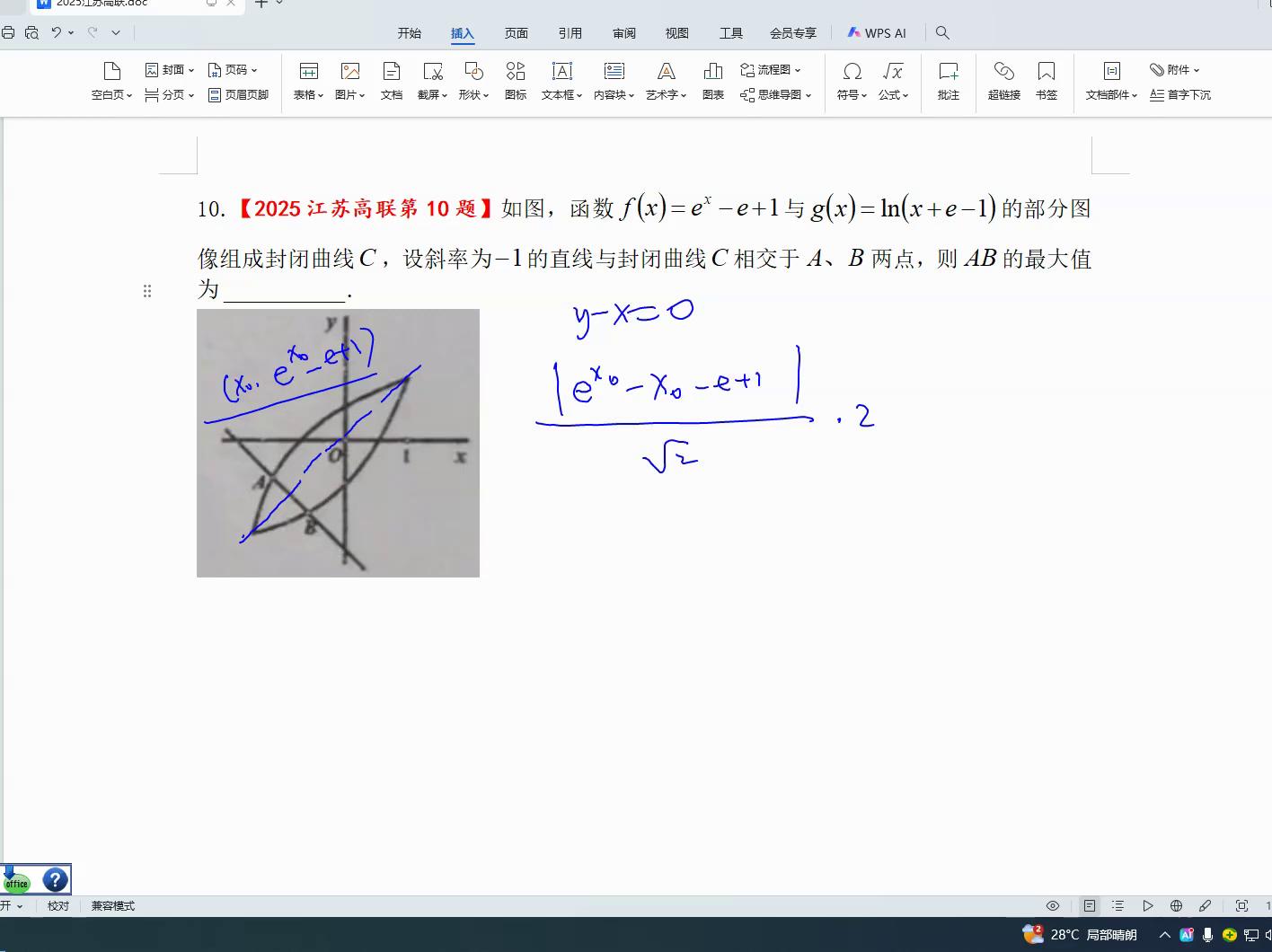
二分之一减去一的结果是负数，二减一的那个位置上是一个负数，four，这个的绝对值最大，显然就是绝对值，就是要取它，绝对值就取这样一个值就可以了。

今天这道视频就分享到这里，谢谢朋友们的观看，再见。