2025江苏高考数学竞赛第3题解析

同学们好，我是高中数学刘老师。今天要分享的视频内容，是二零二五年江苏高考数学竞赛的第三题。这道题目考察的是复数知识，难度不算高，比较容易应对，关键在于它的模不等于零。

要开始简化，简化时可以设c为a与b之和，然后以此方式继续简化。

接着分子分母同乘一个更小的数，或者直接进行相应操作也可以。倘若直接将分子分母乘以某个特定值，比如乘以更小的数即可。由于一个负数乘以更小的数，该负数一旦相乘后会转化为一个非负平方数。

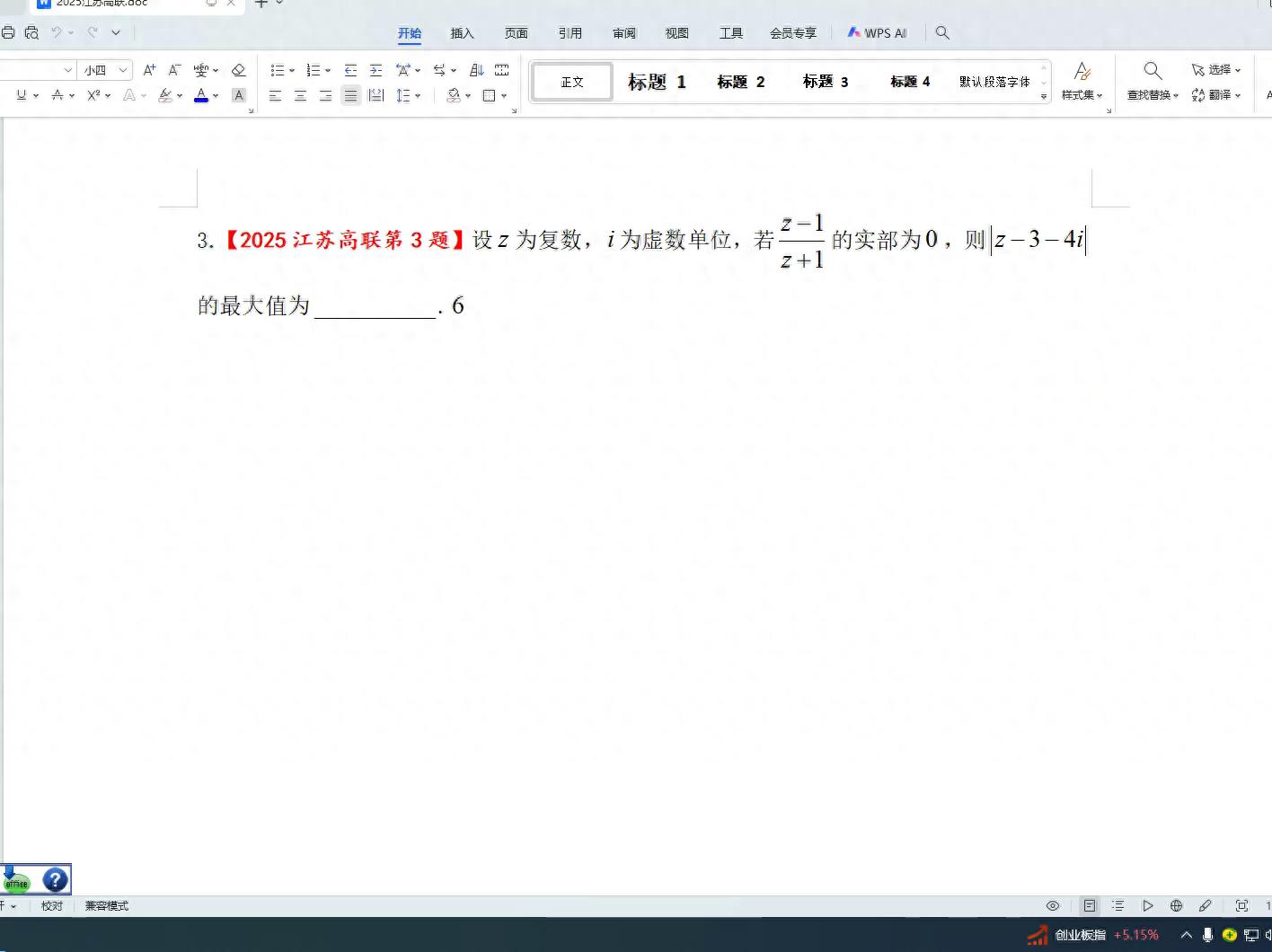
此刻可以忽略分母，分母是模长的平方，模长的平方为正值，因此无需关注。重点考察分子，分析两个相乘时的结果，那是z的模长平方，属于实数范畴。

另外z乘以一，再z乘以一，再减去z，情况更加糟糕，然后还要减去一。这时候就能察觉到，这两个一相减的结果应当是二b i，此处确实是二b i。有人问我为何十不是零，那么就意味着这个位置是二b i，十不为零，仅仅是因为分母是c加一摩长平方。

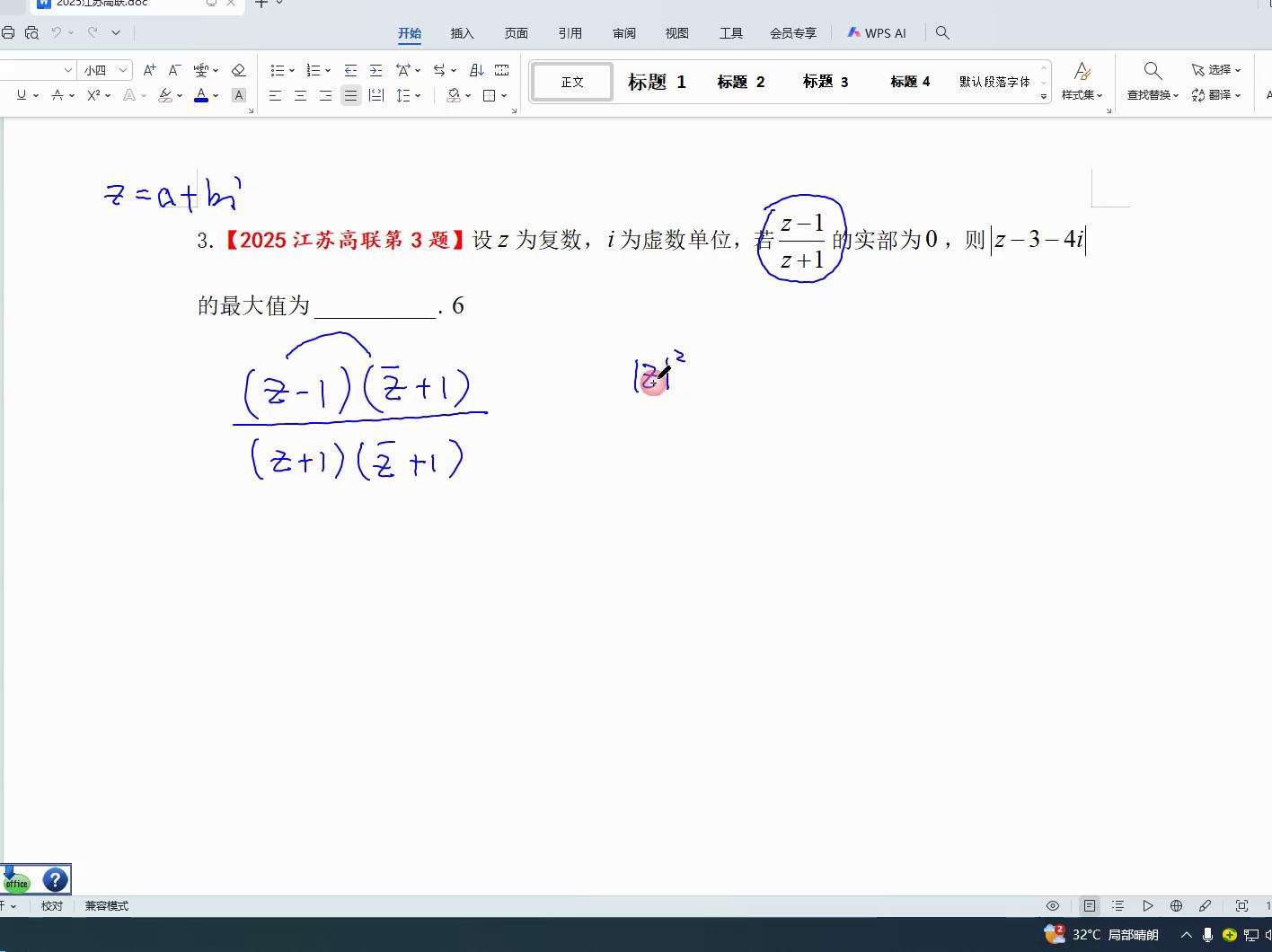
若说它的十不为零，则表明z的模长平方与e相等，由此可知z的模长等于一，这个结论得到了证实，z的模长确实是一。

z的模长是一，这说明了什么，说明了z这个负数到原点的距离是一，是一个单位圆，c的摩擦力就是a平方加b平方等于一，a平方加b平方等于一就是z这个复数的点就在这个圆周上

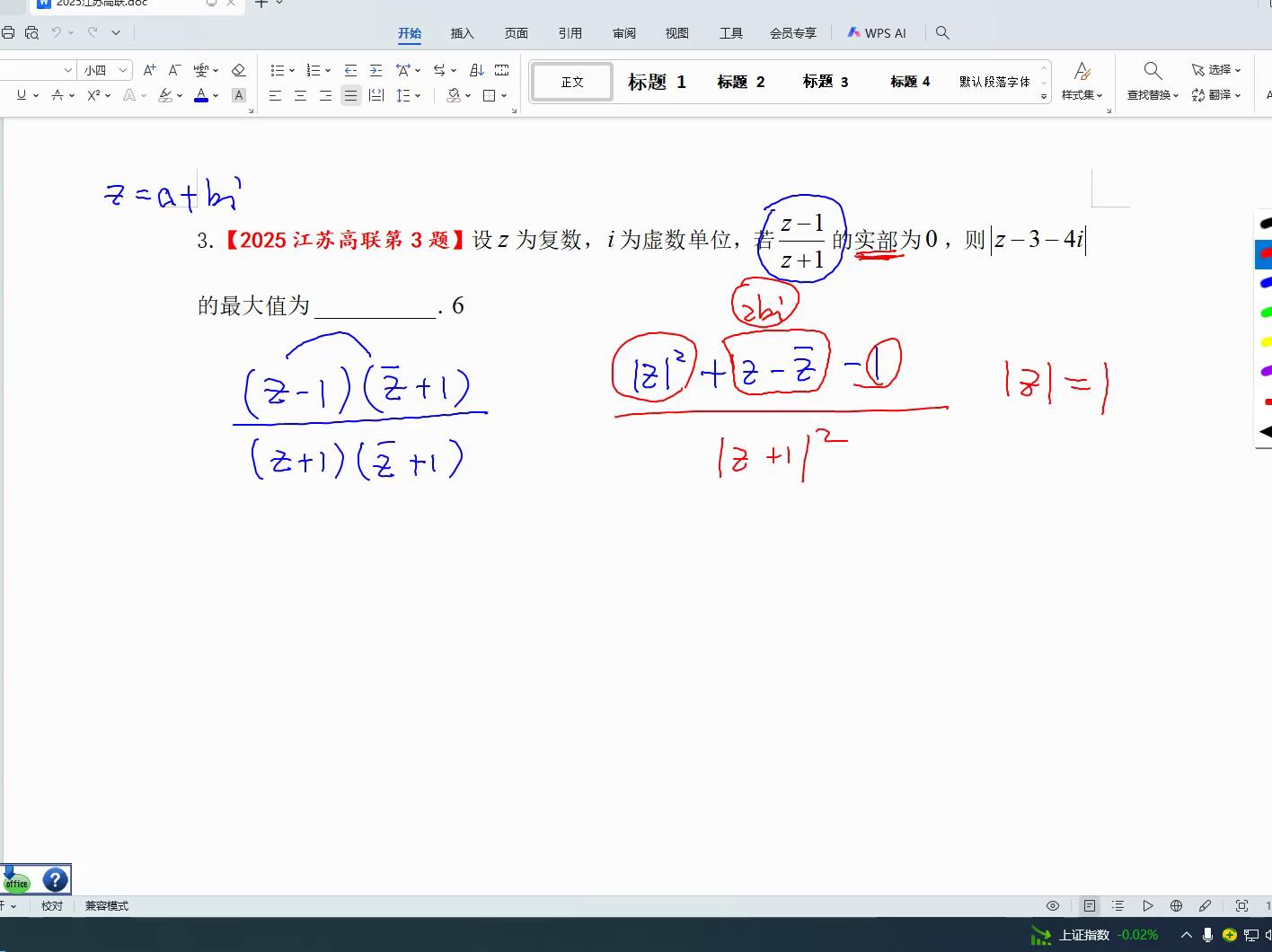
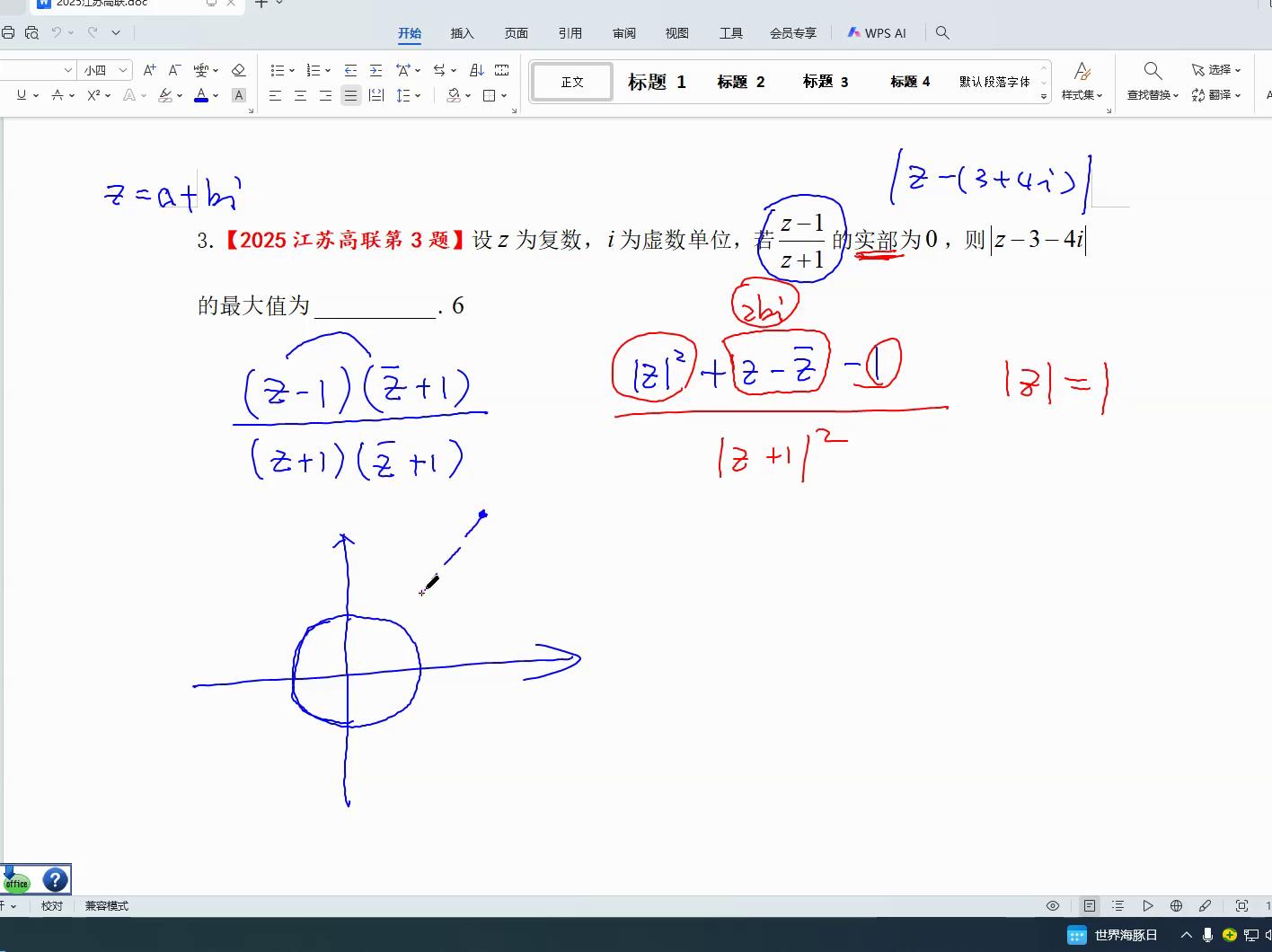
此处是否为z减去三再减去四, z减三减四i代表什么意义？z减去三加上四i, 三加上四i。这种关系说明两个复数在负半轴上的位置, 距离为三和四的点, 显示圆桌上的哪个点与此距离最为远。

很明显需要计算与圆心之间的间隔，然后加上半径，这就是一个点到圆心的间隔再加上半径，这就是最远的距离。圆心之间的间隔因为该坐标是三个四，显然是五，说五加一是六，这是一个最大数值。当然也可能称为确定界限，如果要求界限，那么最大值就是五加一十六，最小值是五减一，等于四，最大值是五加一十六，这就是那个东西。

这是一个基础题目，需要找到z这个负pro特征，它具备何种特性？

今天这道视频就分享到这里，谢谢同们的观看，再见。