2025江苏高中数学联赛第7题解析

各位同学大家好，我是高中数学刘老师。今天要介绍的题目是二零二五年江苏省高中数学竞赛的第七题。这道题目考察的是向量方面的知识，现在开始阅读题目内容。

这个图形是一个直角三角形，其中a和b代表斜边，c、h、c、b是三条边，二二是内心，这表明内心就是内切圆的圆心，然后计算c、r、零二r乘以c、a的值，再加上背带乘以a、b的值，最后求二万加倍的数值。

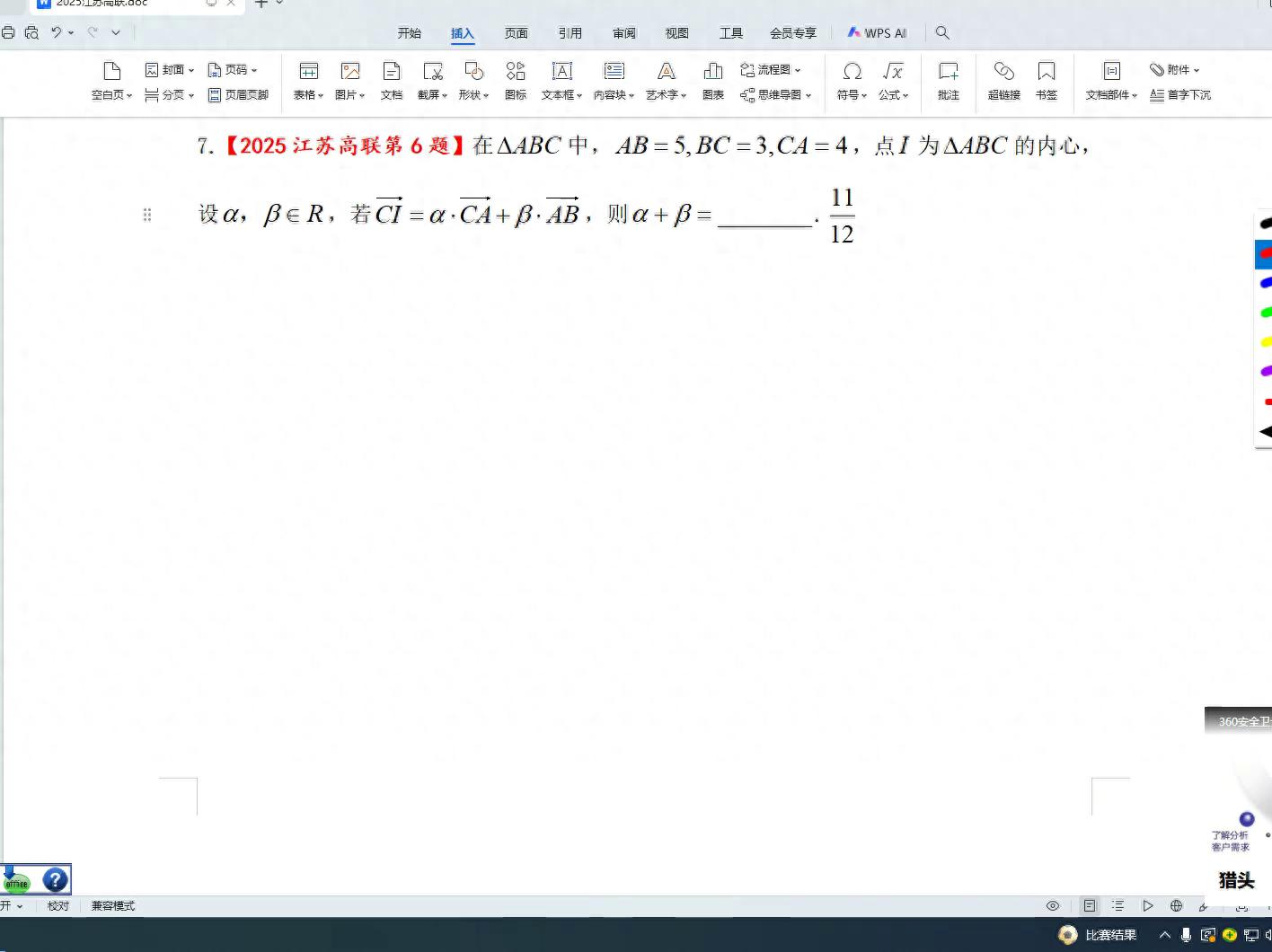
这个要怎样实施呢，显然是借助坐标的途径，需要设定坐标系，让c和a作为x轴基准，让c和b作为y轴基准。接下来核心的步骤是确定i坐标的位置，找到i坐标其实只要测量出半径即可。计算半径是一个比较通用的技巧，可以用计算面积的方式来完成。

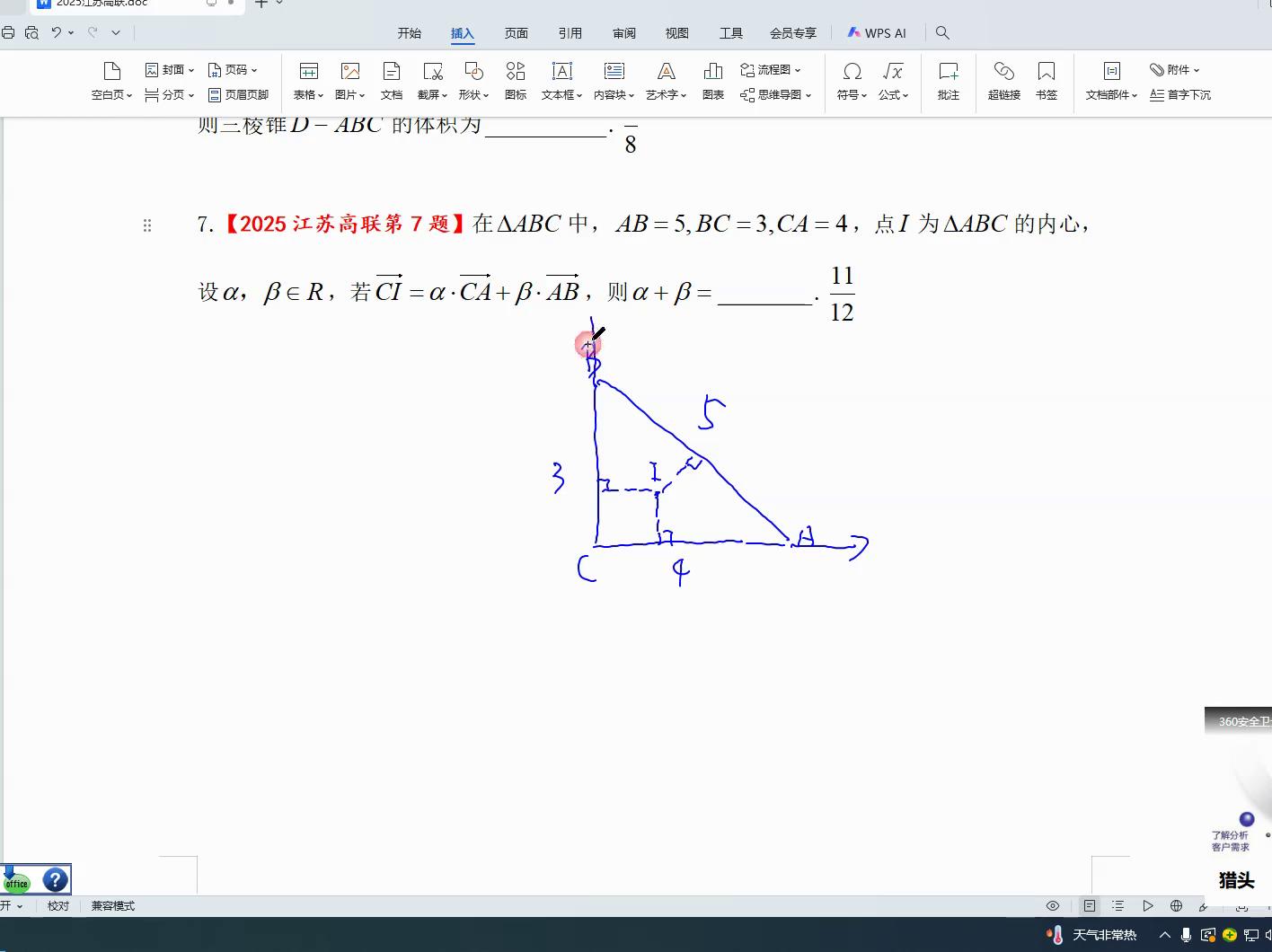
通常通过划分区域将大三角形分割成三个小三角形，将i、b、i、a、i、c依次连接，便形成了一种面积计算方法，即二分之一乘以三乘以四，连接完毕后得到三个三，也就是二分之一乘以括号内的三加四加五乘以h，去掉二分之一后，三乘以四等于十二，三加四加五也等于十二，h的值为一。

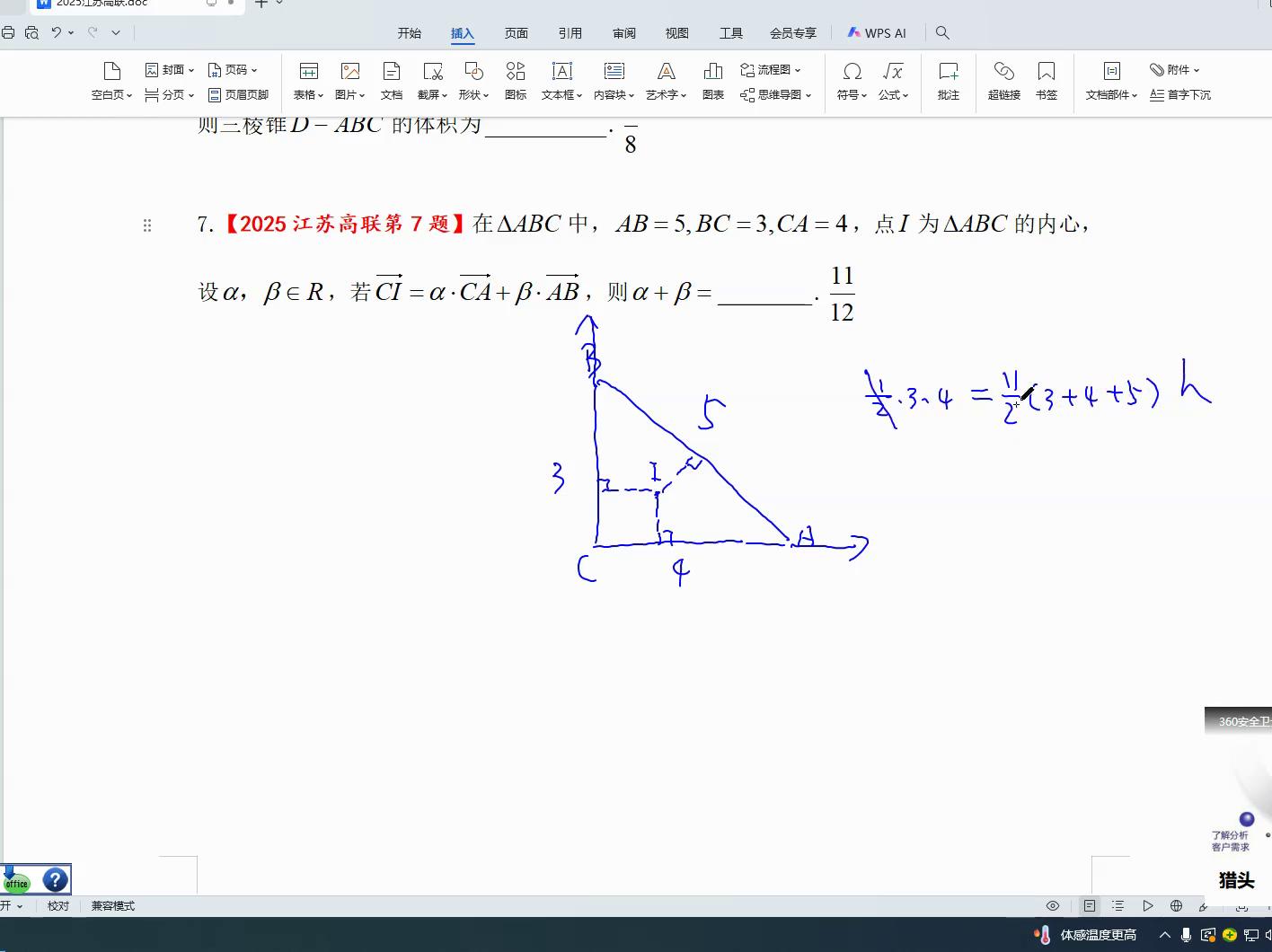
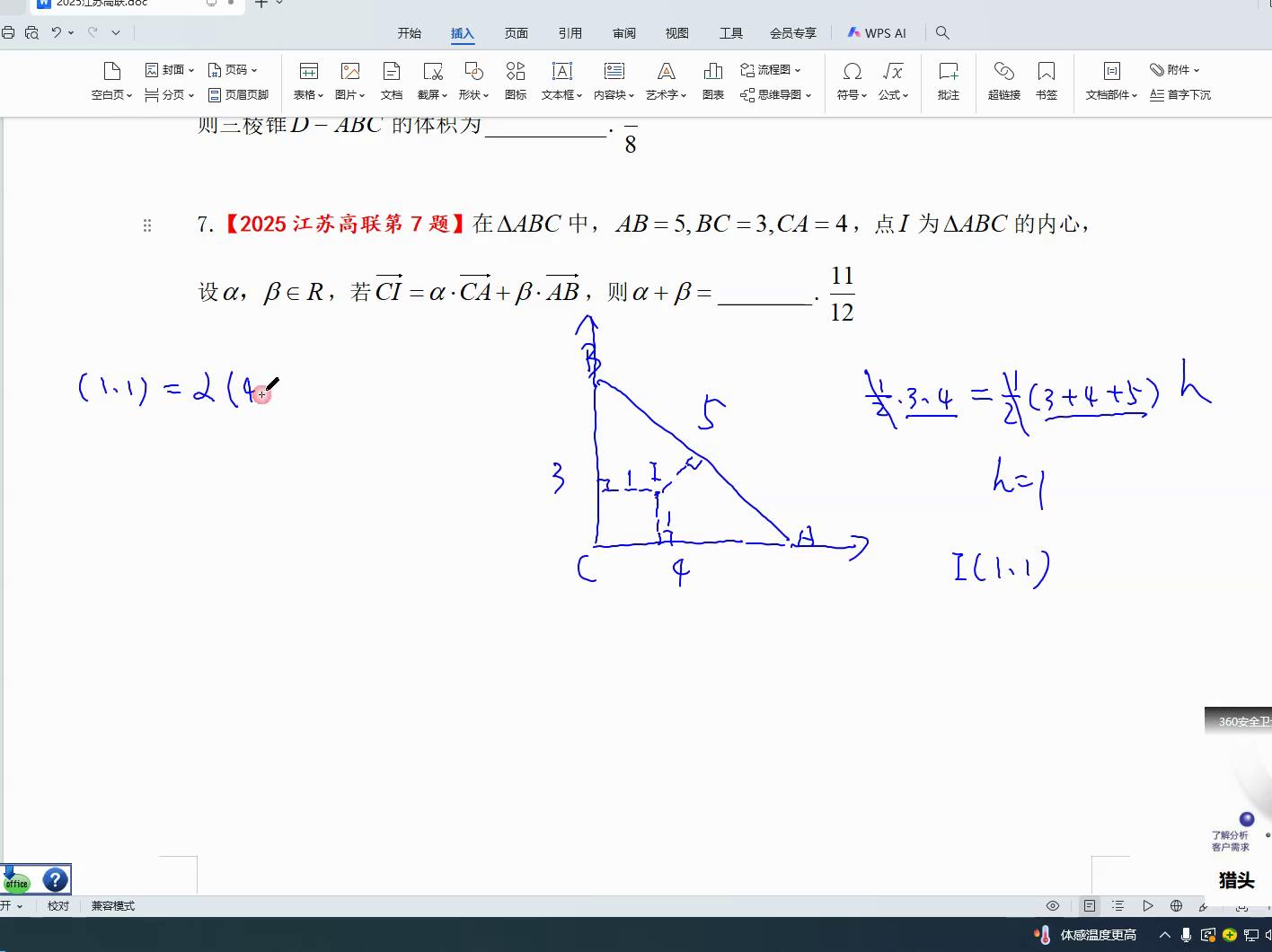
只有求着零千元的半径是一，r、a坐标就是一一了，对不对？这个限量的左侧为某个数值，右侧是alpha与c、a限量的乘积，c、a限量等于四十，再加上bet得到a、b项量，a、b项取b点坐标减去a点坐标结果是负四正三，由此得出四倍的alpha减去bat等于一，接着三倍的bat等于一，这样计算得出bat等于三分之一，阿尔法减备胎等于四分之一，阿尔法值便求出，为三分之一加四分之一，即十二分之七，阿尔法加备胎也就自然得出，等于十二分之十一。

今天这道视频就分享到这里，谢谢朋友们的观看。