2025江苏高中数学联赛第8题解析

各位同学大家好，我是高中数学刘老师。今天要分享的这道视频是二零二五年江苏高中数学联赛的第八题，这是一道概率问题。甲有两个白球，一个黑球，乙有两白一黑，你们是三个白球，现在要经过四次交换，黑球仍在乙处的概率是多少？最后黑球仍在乙处的概率是多少？具体怎么去算？这个应该是概率的递推问题。

推广工作需要确定一个推广模式，用符号p a来代表第n次，第n次出现黑球时增加概率的情况。如果dn次黑球出现在乙处，那么就是1减去pp，dn次黑球出现在乙处的情况。现在需要找到一个具体的模式，具体是什么意思呢？就是要推算一下pn加一次，pn加一次等于什么。p n 执行平牙操作时，有两种可能结果，第一种是第 n 轮黑球位于甲处，第二种是第 n 轮黑球位于乙处，黑球在一，总共有两种情形。

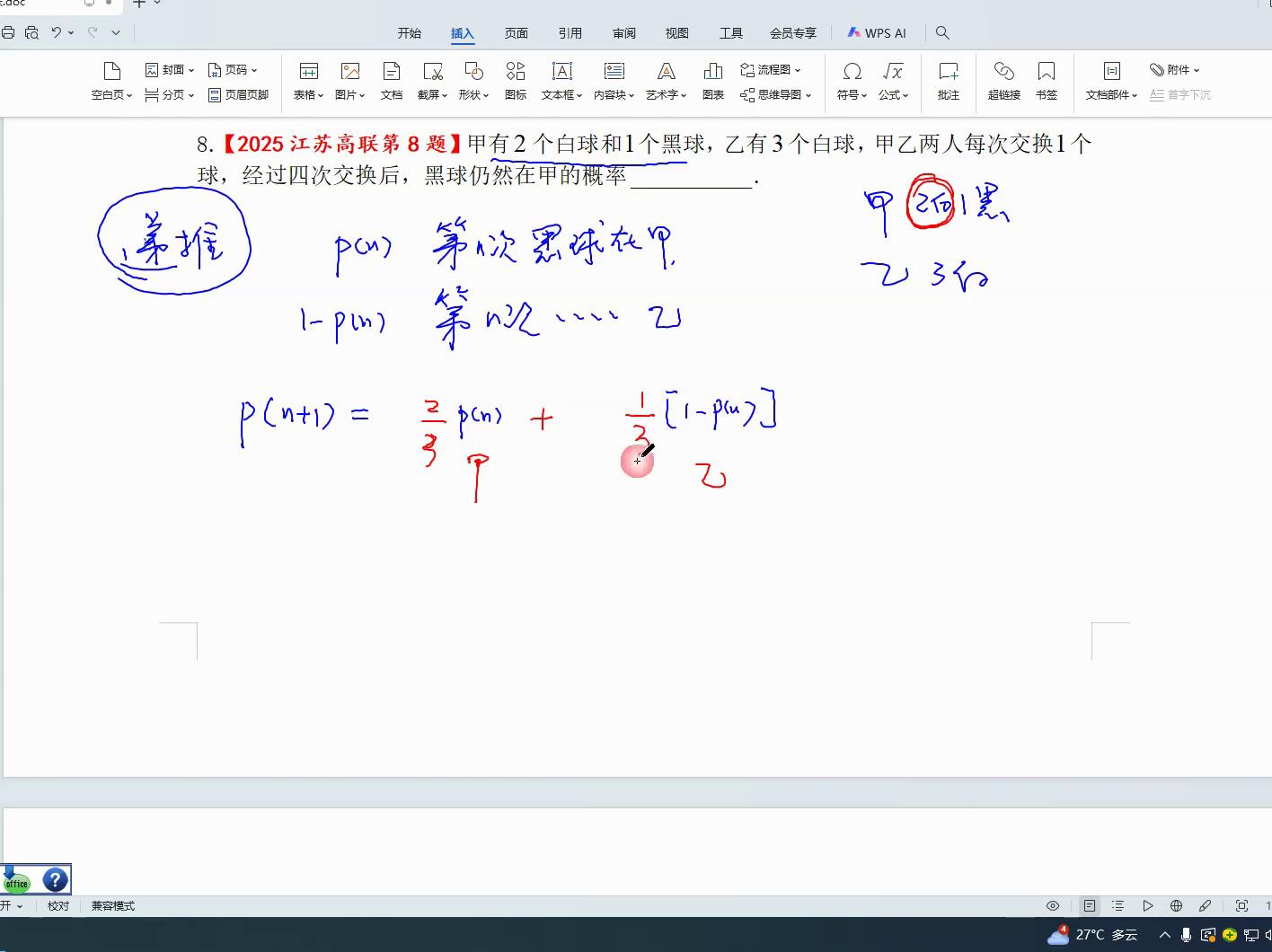
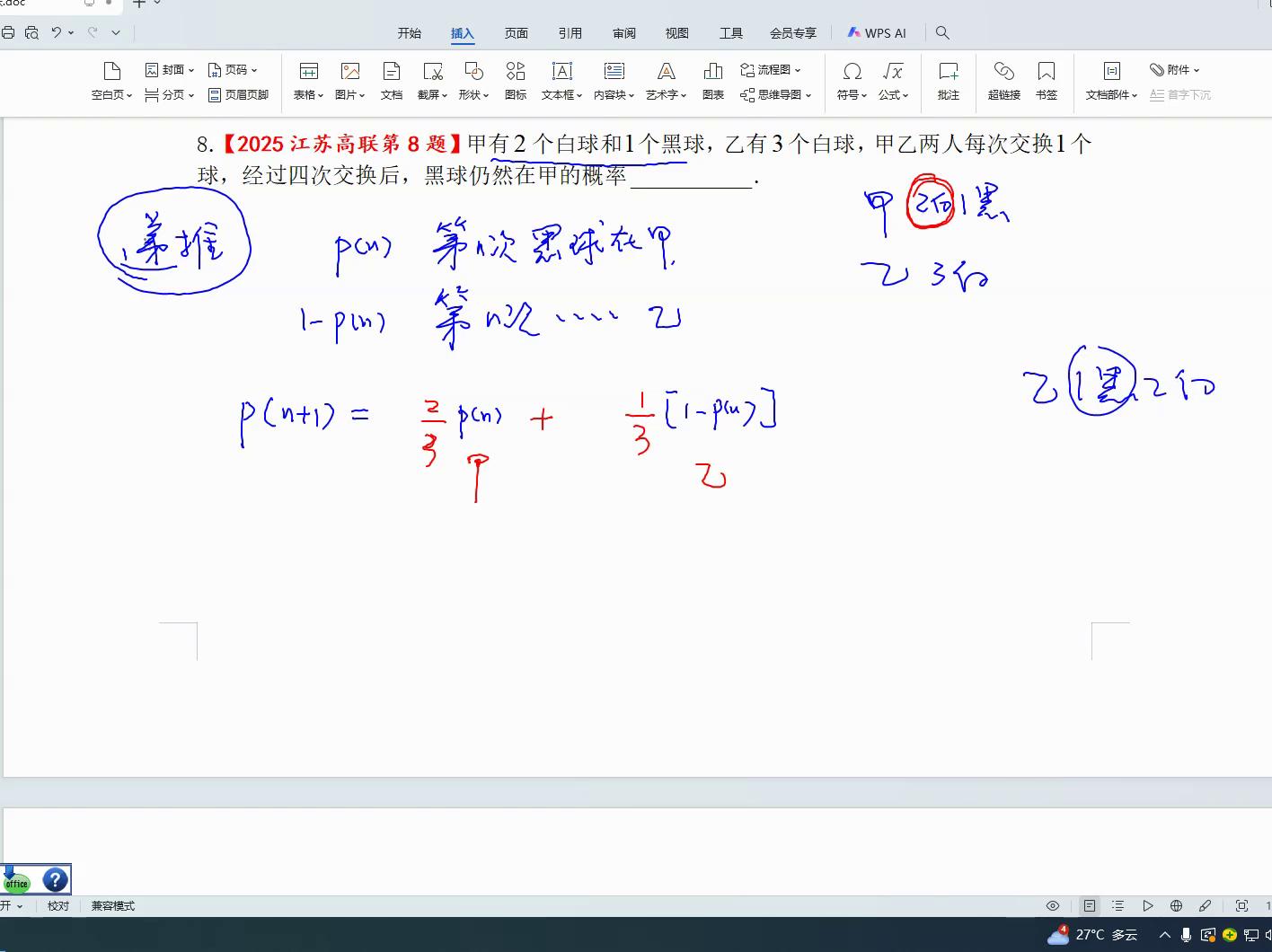
当第n次黑球位于甲处，若需交换，假只能交换白球，因为假手仅持有三个球，故无法交换黑球，此情形下交换概率必定是三分之二，同理，若黑球在乙处，现需将黑球转移至甲，该处交换概率必定是三分之一，黑球必须归还甲处，方能确保dn加一次黑球后再加。

由于黑球位于乙处，黑球位于乙处意味着乙处为一黑两白，若进行交换则必须交换黑球，其概率为三分之一。将此式简化后，便很容易得出三分之一，pa再加上三分之一，再加上三分之一，由此又可推导出逆向公式，获得逆向公式便可以继续逆向推导。

当p为一时，p为一，nk变为零，n变为零即为初始情形，初始情形即为一个，初始情形就p为零是一个，定义就是p为零即为初始情形，再增加它是等于一个，这是三分之二。p二进行计算时就是三分之一乘三分之二，三分之一乘三分之二再加上三分之一，这个计算出来是九分之二，九分之五。

然后求出p三，三分之一同九分之五相乘，接着把二十七分之五加上三分之一，然后计算三分之一除以二十七分之九，结果是二十七分之十四，p四接着用三分之一乘以八十一分之十四，再加上三分之一，最后得到三分之一等于八十一分之二十七，由此可以轻易求出八十一分之四十一，这就是最终结果，发现了一种地推的关联。这道题的一个观念要能推出来这样一个地推公式。

今天的试题就分享到这里，谢谢同学们的观看，再见。